Abb. 1
Portugal - Degrees of darkness - %_of_Pop_by_age_>=65
Kartographische Visualisierung
Choroplethenkarten
Degrees of
darkness
Entfernung von Ausreißern aus der
Präsentation
Klassifikation
Standalone bars
Color
Parallel bars
Pies
Triangles
Utility bars
Utility wheels
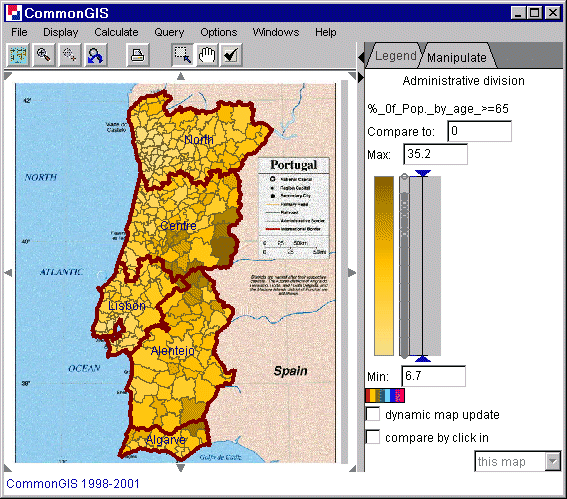
Die Visualisierungsmethode von Choroplethenkarten basiert darauf Werte eines Attributes bezogen auf eine Fläche durch Farben oder Schattierungen darzustellen. "Unclassed" (nicht klassifiziert) bedeutet, daß numerische Attribute ohne vorherige Klassifizierung in Farbschattierungen umgewandelt werden: der Grad der Dunkelheit ist (in etwa) proportional zum Wert, der repräsentiert wird. Ein Vorteil von Choroplethenkarten ist der Überblick, den man über die räumliche Verteilung der Daten bekommt. Da die gesamte Verteilung in einem Bild zusammengefaßt werden kann, kann man auch zwei oder mehrere Verteilungen auf einmal mit Choroplethenkarten betrachten. Solche Vergleiche machen Zusammenhänge zwischen mehreren Variablen oft deutlicher: Ähnlichkeiten werden durch gleichartige Muster sichtbar.
In einer sogenannten nicht klassifizierten Choroplethenkarte werden numerische Attributwerte in annähernd proportionalen Farbschattierungen dargestellt: Je größer der Wert, desto dunkler die darstellende Farbschattierung.

Abb. 1
Portugal - Degrees of darkness -
%_of_Pop_by_age_>=65
Manchmal ist bei einer solchen Karte eine zweiseitige, oder zweigeteilte Farbskala dabei, um zwischen den Werten über und unter einem Referenzwert (Mittelpunkt) zu unterscheiden: sie wird in unterschiedlichen Farben, zum Beispiel braun und blau unterteilt. Eine extra Farbe, zum Beispiel weiß repräsentiert Werte, die genau gleich dem Referenzwert sind. Descartes ermöglicht es interaktiv den Referenzwert zu ändern und diese Änderung direkt auf der Karte zu sehen. Diese Operation ("visual comparison" genannt) verdeutlicht räumliche Strukturen, unterstützt den geographischen Vergleich der Objekte, und erleichtert das Auffinden von bestimmten Werten auf der Karte. Dazu verschiebt man den zweiseitigen Pfeil an der Farbskala auf die gewünschte Position (ist das Feld "dynamic map update" aktiv, so erscheinen die Veränderungen sofort auf der Karte), oder man klickt auf ein Objekt mit dem Referenzwert (vorher noch "comapre by click in" aktivieren und "this map" auswählen, wenn nur von der Karte ein Referenzwert erscheinen soll).
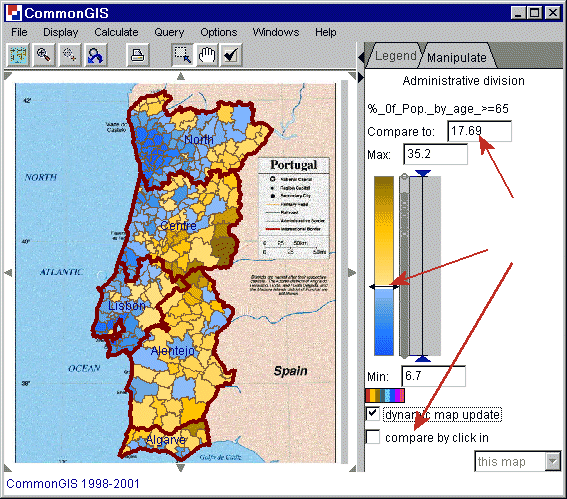
Abb. 2
Portugal - Degrees of darkness -
%_of_Pop_by_age_>=65
Um räumliche Strukturen und Tendenzen zu erkennen, kann man den zweiseitigen Pfeil über die gesamte Skala ziehen. Beobachten Sie die von zwei Farben erscheinende Struktur, unabhängig von der Schattierung. Zum Beispiel in Abb. 2 kann man sehen wie sich die Blauschattierungen (stimmt mit niedrigen Werten überein) zuerst auf die Regionen größerer Städte Portugals wie Lissabon und Porto verteilt, sich dann entlang der Küste und erst dann in das Innere des Landes ausbreitet.
Bestimmte Werte auf der Karte findet man wenn im Textfeld "Compare to" einen Wert explizit angibt. Der Attributwert der Objekte welche dann in weiß gezeichnet sind, stimmen genau mit dem angegebenen Wert überein.
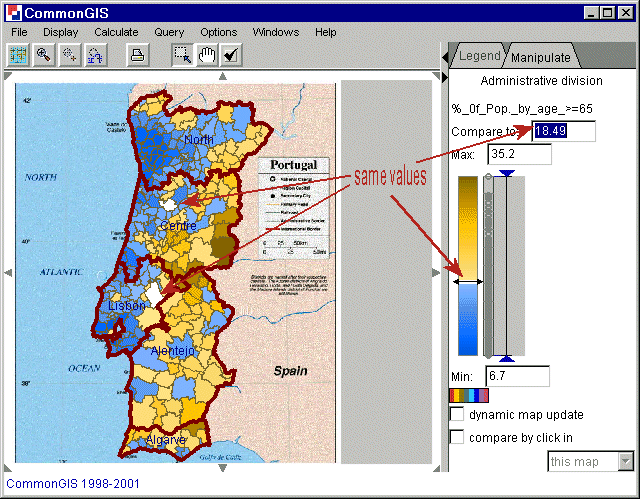
Abb. 3
Portugal - Degrees of darkness -
%_of_Pop_by_age_>=65
Um ein Objekt mit den anderen zu vergleichen, zum Beispiel mit seinen Nachbarn, reicht ein Mausklick darauf. "Compare by click in" sollte aktiv sein. Der Attributwert dieses Objektes wir dann zum Referenzwert. Die Objekte, welche einen höheren Wert haben werden in braun dargestellt, mit niedrigeren Werte in blau. Diese Farben können aber auch geändert werden, indem man auf die Farbtafel unter dem Textfeld "Min" klickt.
Der Punktegraph stellt die Verteilung der Werte dar. Bezüglich des dargestellten Attributes steht ein Punkt für den Wert eines Objektes. Wenn die Maus einen Punkt berührt, so wird dieser, und alle andern Darstellungsmethoden dieses Objektes, hervorgehoben. Abb. 4 zeigt eine Beschreibung der dargestellten Elemente. Die Begrenzungssymbole (kleine blaue Dreiecke genannt "delimiter") werden dazu benutzt um Ausreißer aus der Präsentation zu entfernen. Dies wird im Folgenden noch näher beschrieben.
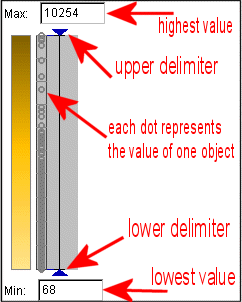
Abb. 4
Dot plot Erklärung
Entfernung von Ausreißern aus der Präsentation:
Sehr oft enthält die zu untersuchende Datenmenge ein paar sehr hohe oder sehr niedrige Werte eines numerischen Attributs, während die restlichen Werte relativ nah beieinander liegen. Solche Werte werden Ausreißer genannt. Zum Beispiel die Geburtenrate in Europa liegt zwischen 10.56 und 14,51 pro 10000, wogegen ein einziges Land eine Geburtenrate von 21.70 vorweisen kann. Karten, sowie andere geographische Darstellungen, die solche Daten darstellen, sind nicht aussagekräftig genug, da der Unterschied zwischen den Werten nicht deutlich wahrnehmbar ist. Die Entfernung von Ausreißern aus der Präsentation ermöglicht es nah beieinander liegende Werte auf eine detailliertere Schattierungsskala zu projizieren, um somit die Unterschiede deutlicher zu machen.
Mit Descartes kann man die Ausreißer so entfernen: Der Benutzer muß die dreieckigen Begrenzer (delimiter, auf der rechten Seite der Karte) so verschieben, daß die unerwünschten Werte außerhalb der grau schattierten Zone liegen. Die Veränderungen werden direkt auf die Karte übertragen. Die neuen Extremwerte werden simultan angezeigt.
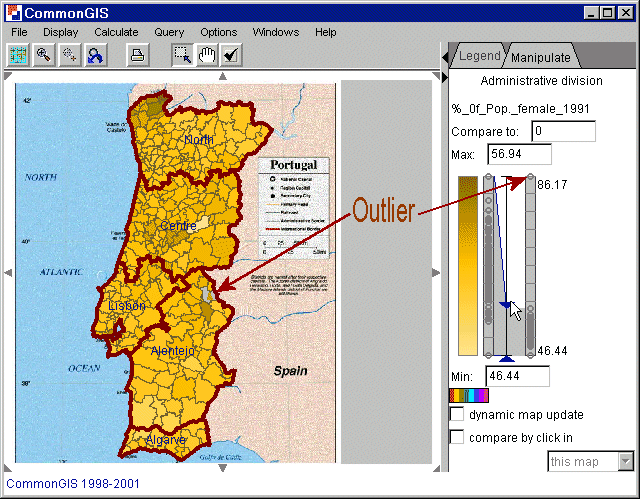
Abb. 5
Portugal - Entfernung von Ausreißern -
%_of_Pop_by_age_>=65
Abb. 5 präsentiert den prozentualen Anteil der Frauen zur Bevölkerung in 1991. Es gibt einen Ausreißer mit einem Wert von 86,11 (Dargestellt auf der Karte mit einer Grauschattierung und einem braunen Dreieck). Auf der rechten Seite des Fensters sind zwei Punktegraphen dargestellt. Der rechte zeigt de gesamten Wertebereich an, wogegen der linke den präsentierten Wertebereich vergrößert angibt (Abb. 6). Descartes zeigt nun nur noch die Werte an, die zwischen den beiden Begrenzern liegen (auf der Karte und im vergrößerten Bereich).Im Beispiel wird nun nach der Entfernung des Ausreißers der höchste Wert (56,94 - angezeigt im Textfenster "Max") mit der dunkelsten Braunschattierung dargestellt.
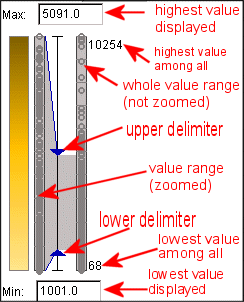
Abb. 6
Dot plot Beschreibung
Die Entfernung von Ausreißern ist auch in anderen Visualisierungsmethoden (standalone bars, bar charts, etc.) möglich.
Eine weit verbreitete Methode kartographische Karten mit numerischen Attributen darzustellen, ist eine klassifizierte Zeichnung. Bei dieser Methode wird der Wertebereich des Attributs in Intervalle unterteilt, welchen verschiedene Farben zugeordnet sind. Die zugehörigen geographischen Objekte werden ebenso auf der Karte in der jeweiligen Farbe gezeichnet.
Die Hilfsprogramme enthalten direkte Manipulationselemente willkürliche Grenzen zu setzen, Graphen welche die statistische Verteilung der Attributwerte darstellen, Hilfsmittel zur automatischen Klassifizierung, Berechnung von statistischen Qualität der Klassifikation und verschiedene Farbpläne, die zur Darstellung der Klassen auf einer Choroplethenkarte angewendet werden können.
Historisch gesehen, wurde Klassifikation zur Minimierung der
Farbenanzahl benutzt, welche für die Darstellung der Datenwerte auf der
Karte nötig waren. Dieses Ziel und die Aufgabe die Subjektivität der
Datendarstellung zu minimieren führten zu der Entwicklung von 3 weit
verbreiteten Methoden von Datenklassifizierung (Abb. 7):
1) Klassifikation
in gleich große Intervalle;
2) Klassifikation mit einer
Gleichverteilung der Objekten in den Klassen;
3) Statistisch optimale
Klassifikation.
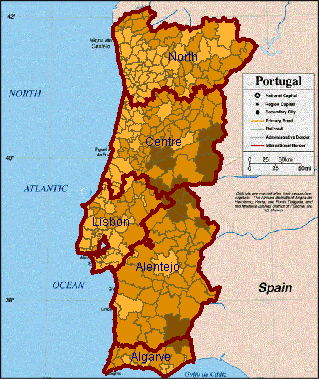
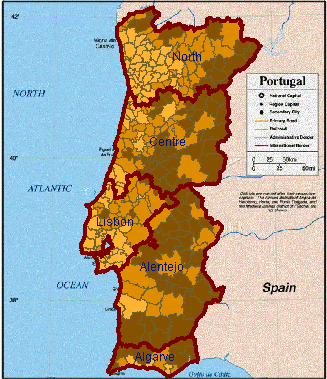
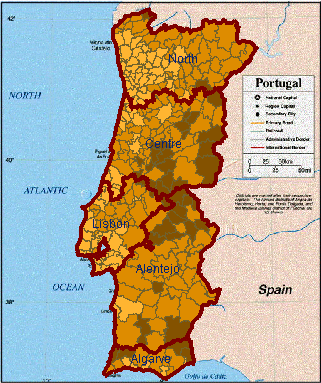
Abb. 7
Portugal - Varianten der Klassifikation
von "%_Of_Pop_by_age_>=65": gleich große Intervalle, gleich verteilte
Klassifikation, und statistisch optimale Klassifikation
Es ist in Kartographie wohlbekannt, daß eine unterschiedliche Anzahl der Klassen und der Umbrüche die Information der Karte gründlich ändern können. Dies wird zum Beispiel bei dem Vergleich der Choroplethenkarten in Abb. 7 deutlich. Diese Karten resultieren aus 3 verschiedenen Variationen der Klassifikation in 3 Klassen von Regionen in Portugal je nach Wert des Attributs "%_Of_Pop_by_age_>=65". Dennoch ist es schwer zu glauben, daß die selben Daten benutzt wurden. Der Effekt von Klassifikation kann verdeutlicht werden, wenn diese Karten mit nicht klassifizierten Choroplethenkarten des selben Attributs darstellt werden (Abb. 1).
Es gibt folgende Hilfsprogramme zur Klassendefinition:
1)
Automatische Klassifizierung: Klassifikation in gleich große Intervalle,
Klassifikation mit einer Gleichverteilung der Objekten in den Klassen,
Statistisch optimale Klassifikation. Diese Methoden können auf zwei Weisen
benutzt werden: Der Benutzer kann entweder die gewünschte Anzahl der
Klassen angeben, oder die gewünschte Qualität. Letzeres entscheidet
selbst über die Anzahl der Klassen. Um diese Methoden dann anzuwenden
klickt man auf "run".
2) Eine Texteingabe welche die momentanen Werte der
Umbrüche angibt. Umbrüche können an dieser Eingabe
verändert, entfernt, oder hinzugefügt werden.
3) Ein
zusammengesetzter Schieber, welcher visuell die relativen Positionen der
Klassenumbrüche innerhalb des Minimal- und Maximalwertes des Attributes
und die momentan benutzten Farben anzeigt (Abb. 8). Ein Punktegraph gehört
zur Anzeige dazu, welche die statistische Verteilung der Attributwerte
angibt.
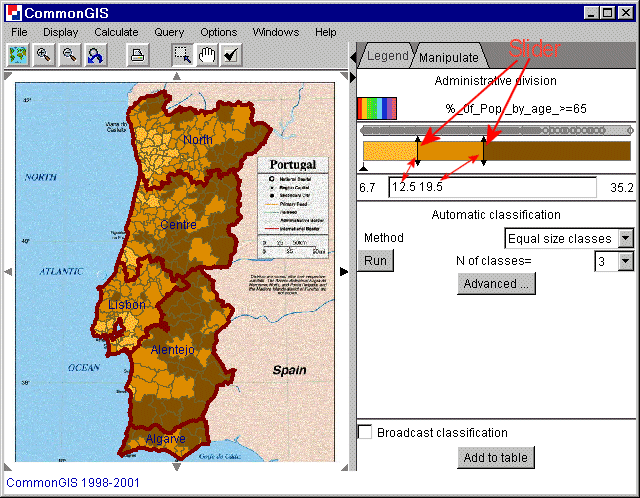
Abb. 8
Portugal - Klassifikation - %_of_Pop_by_age_>=65
Der zusammengesetzte Schieber ist eine direkte Manipulationssteuerung.
Die Zeiger können bewegt werden und verändern somit auch die
Klassifikation. Wenn ein Zeiger einen benachbarten Zeiger annähert. so
wird dieser entfernt (d.h. zwei aufeinanderfolgende Klassen werden
zusammengefaßt). Wenn auf eine freie Fläche zwischen zwei Zeiger
geklickt wird, so wird ein neuer Zeiger hinzugefügt, der diese Klasse in
zwei neue Klassen unterteilt.
Der zusammensetzte Schieber hat eine
spezielle Funktion: Während des Prozesses des Bewegens eines Zeigers,
werden nur die Objekte der zwei sich ändernden Klassen auf der Karte
angezeigt. Alle anderen Objekte werden in einem neutralen grau gezeichnet. Dies
ermöglicht es, sich auf die resultierenden Änderungen der
räumlichen Muster besser zu konzentrieren.
Alle Bilder werden sofort
nach jeder Veränderung der Klassen, insbesondere während
der Bewegung eines Zeigers, aktualisiert.
Als Ergebnis einer jeden Klassifizierung ist mit dem Verlust von
Genauigkeit zu rechnen. Der Genauigkeitsverlust (nämlich der statistische
Fehler durch die Klassifizierung) kann gemessen werden. Der gesamte Fehler
einer Klassifizierung ist als Summe von internen Fehlern für jede Klasse,
E=ΣEk, zu verstehen. Der interne Klassenfehler Ek hängt von der
gewählten Norm ab. Es werden 3 Normen eingeführt namens "mean
measure", "median measure", und "entropy measure".
Die erste Norm wird als
quadratische Abweichung vom Klassenmittelpunkt Ek= Σ(Xi-Xk)^2
berechnet, wobei Xk der Klassenmittelpunkt ist. Die zweite Norm wird als Summe
von absoluten Abweichungen vom Klassenmedian berechnet,
Ek=Σabs(Xi-Xk), wobei Xk der Klassenmedian ist. Diese Norm ist im
Vergleich zu der ersten Norm weniger von Verteilung (Ausreißer)
beeinflußbar, da die Randdaten weniger Einfluß auf den Median als
auf den Mittelwert. Die dritte Norm beruht auf die Abweichung vom Mittelwert
welche mit einer Logarithmusfunktion des informationstheoretischen Ansatz
berechnet wird, Ek=Σabs(Xi-Xk)log(abs( Xi-Xk+1)). Falls die
Abweichung klein ist, wächst die Funkton zunächst wie der Mittlere
quadratische Abstand (die erste Norm), während sie für große
Abweichungen sehr viel langsamer wächst, so daß die Ausreißer
den Gesamtfehler weniger beeinflussen.
Für jede Klassifikation vom System produziert, oder vom Benutzer
modifiziert, werden 2 Qualitätsindikatoren berechnet. Die erste
repräsentiert den Verlust der Genauigkeit durch die Klassifikation. Die
zweite ist das Verhältnis des ersten Wertes und des Wertes für die
statistisch optimale Klassifikation mit der selben Anzahl von Klassen. Demnach
drückt der erste Indikator aus, wie weit die Klassifikation sich von den
original Daten entfernt und der zweite wie weit sie sich von der optimalen
Klassifikation entfernt ist. Um die optimale Klassifikation zu finden, wird ein
Algorithmus benutzt, welcher eine spezielle iterative Organisation welche
Klassifizierungen von vorhergehenden Schritten effizient auf den nächsten
Schritt anwendet.
Beide Qualitätsindikatoren werden als Nummer
gemessen an einer Skala von 0% bis 100% und als Grafik (Abb. 9) dargestellt.
Die Indikatoren werden automatisch aktualisiert, nach jeder Veränderung
der Klassen.

Abb. 9
Präsentation der statistischen
Qualität einer Klassifizierung
Bei der Klassifizierung von räumlichen Daten sollte ein Analytiker die Daten aus zwei Perspektiven betrachten, den statistischen und räumlichen, sowie die Eigenheiten der Verteilung der Daten. Dies bedeutet, daß der Analytiker mindestens zwei Ziele gleichzeitig verfolgen muß. Das erste ist die Variation der Daten in jeder Klasse zu minimieren und die Unterschiede zwischen den Klassen zu maximieren. Das zweite Ziel ist es die Gebiete in die kleinste mögliche Anzahl von kohärenten Regionen mit einer möglichst geringen Datenvariation zu unterteilen. Der Analytiker braucht Hilfsmittel welche ihm/ihr erlauben die Balance zwischen diesen Zielen auf der Suche nach akzeptablen Kompromißlösungen zu bewahren. Wohingegen der Algorithmus der statistischen optimalen Klassifikation nur dem ersten Ziel gerecht wird und die räumlichen Aspekte der Daten außen vor läßt, und somit dem zweiten Ziel nicht nachkommt. Deswegen ist die oben beschriebene "Freihand" Klassifikation so wichtig: Klassenumbrüche können verschoben werden und die Veränderungen können auf der Karte beobachtet werden. Eine visuelle Darstellung der statistischen Werteverteilung kann dem Analytiker helfen die statistischen Kriterien im Laufe der interaktiven Klassifizierung zu finden. Der Punktegraph neben dem zusammengesetzten Schieber kann dafür hilfreich sein, aber das Überlappen der Punktsymbole kann das Verständnis der Verteilung trüben.
Eine weitere Methode der graphischen Präsentation von statistischer Verteilung, ist die "cumulative frequency curve" (anwachsende Häufigkeitskurve) oder "ogive". In solch einem Graphen werden auf der horizontalen Achse die Attributwerte dargestellt. Die vertikale Position eines jeden Punktes der Kurve entspricht der Anzahl der Objekte mit Attributwerten kleiner oder gleich dem Wert, welher von der horizontalen Position dieses Punktes repräsentiert wird. Eigenheiten von Werteverteilungen können von der Form der "ogive" wahrgenommen werden. Steile Segmente entsprechen Anhäufungen von nah beieinander liegenden Werten. Die Höhe eines solchen Segmentes zeigt die Anzahl der nah beieinander liegenden Werte. Horizontale Segmente entsprechen der "natürlichen Umbrüche" in der Sequenz der Werte.
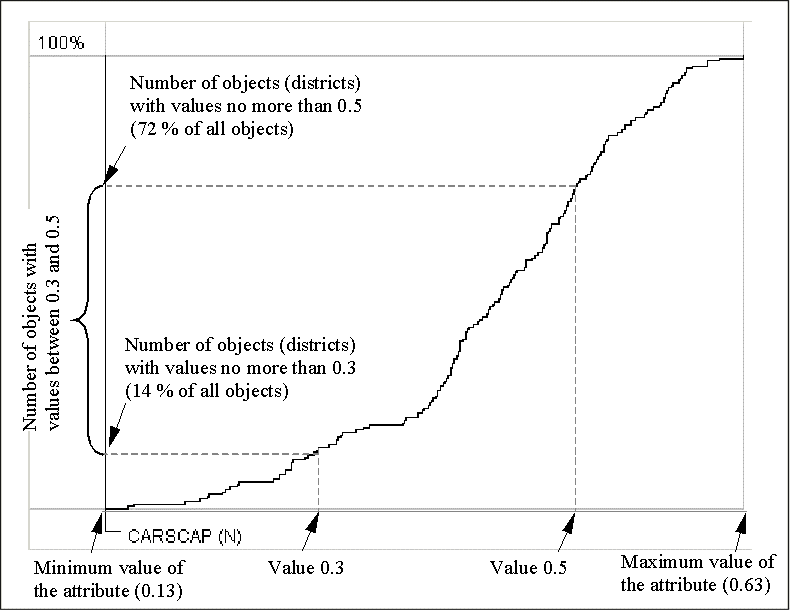
Abb. 10
Cumulative frequency curve
Es ist wichtig, daß die cumulative frequency curve keine frühere Klassifizierung benötigt. Jedoch kann es Resultate einer Klassifikation mit zusätzlichen graphischen Elementen darstellen. Dadurch eignet sich die horizontale Achse des Graphen dazu die Klassenumbrüche anzuzeigen. Hierfür benutzt Descartes segmentierte Barren, deren Segmente die Klassenintervalle darstellen. Die Segmente sind in der Farbe der Klasse bezeichnet. Die Positionen der Umbrüche werden auf die Kurve projiziert und die zugehörigen Punkte der Kurve projizieren die Umbrüche wiederum auf die vertikale Achse. Die Unterteilung der vertikalen Achse wird auch in den Farben der Klassifizierung wiedergegeben. Die Länge der Segmente sind proportional zu der Anzahl der Objekte in der entsprechenden Klassen. Mit solch einer Konstruktion kann man einfach die Größen der Klasse besser vergleichen. Zum Beispiel die Klassenumbrüchen in Abb. 11 unterteilen die gesamte Menge der Objekte in 3 Gruppen von ungefähr gleicher Größe, welche durch gleich große Längen der Achsensegmente auf der vertikalen Achse verdeutlicht wird.
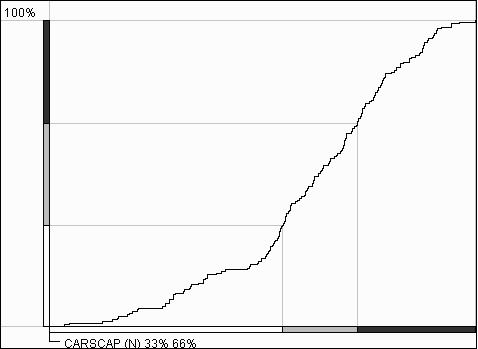
Abb. 11
Klassen in einer cumulative
frequency Kurve
Die Nutzung der Karte und der cumulative frequency Kurve, zusammen mit dem Hilfsmittel der Klassifikation, erlaubt dem Benutzer die Balance zwischen statistischen und geographischen Kriterien zu halten. Zum Beispiel, nach der Betrachtung des Graphen in Abb. 11 könnte man den unteren Umbruch von dem geballten Gebiet (dargestellt durch ein steiles Segment der Kurve) zu dem horizontalen Segment links davon schieben wollen. Diese Operation würde die Klassifikation vom statistischen Standpunkt aus verbessern. Wenn ein Umbruch bei einer flacheren Steigung ist, könnte es angemessen sein die Grenze um diese Position herum zu verschieben, um ein einfacheres räumliches Muster zu erhalten. Es ist auch möglich während des Verschiebens der Umbrüche sein Augenmerk auf die vertikale Achse zu richten und Klassen mit der gewünschten Größe zu erhalten (Anzahl der Objekte).
Bei bestimmten Anwendungsbereichen könnten zusätzliche Klassifikationskriterien zu der Verknüpfung mit statistischen und geographischen Kriterien eine Rolle spielen. Zum Beispiel, in demographischen Analysen kann es wichtig sein Klassen von Bezirken zu produzieren, welche sich nicht zu sehr von der Gesamtzahl der Bevölkerung die dort wohnt, unterscheidet.
Es ist möglich die Idee der cumulative frequency Kurve zu verallgemeinern und ähnliche Graphen zu erstellen, welche beliebig viele Attributwerte summieren. Beispiele solcher Attribute sind Gebiete, Populationsgrößen, Bruttosozialprodukt, Anzahl der Haushalte, etc. Eine verallgemeinerte cumulative Kurve kann folgendermaßen erstellt werden: Sei auf der horizontalen Achse das Attribut A und auf der vertikalen das Attribut B abgebildet. Die Kurve weist jedem Wert x von A die Summe der Werte von B zu, welche für die Objekte mit den Werten von A berechnet wurden und kleiner oder gleich x sind. Demnach entspricht der maximale Wert von A der Summe der B-Werte aller jeweiligen Objekte. Seien zum Beispiel die Bezirke von Leichestershire bezüglich der Anzahl der Autos pro Kopf klassifiziert und eine verallgemeinerte cumulative Kurve stelle das Attribut "Total population" (absolute Bevölkerung) dar. Dann würde die vertikale Position von x Autos pro Kopf die Anzahl der Personen, die in einem Bezirk mit mehr als x Autos pro Kopf wohnen, widerspiegeln.
Das Klassifikationsprogramm von Descartes erlaubt das Hinzufügen einer verallgemeinerten Kurve für jedes quantitative Attribut zu der "cumulative frequency curve" Darstellung. Die Kurven werden übereinander in dem selben Fenster (siehe Abb. 12) gezeichnet. Um die Kurven besser zu unterscheiden werden sie in unterschiedlichen Farben dargestellt. Die horizontale Achse bleibt für alle gleich. Die vertikalen Achsen werden nebeneinander auf der linken Seite des Graphen gezeigt. Jede der vertikalen Achse ist in die selbe Anzahl von Segmenten unterteilt, aber die Positionen der Umbrüche sind im allgemeinen verschieden. Dies wird in Abb. 12 deutlich. Es zeigt daß 34 % aller Bezirke in die untere Klasse der Klassifikation passen. Sie beanspruchen nur 10 % der Gesamtfläche, enthalten aber 50 % der gesamten Bevölkerung.
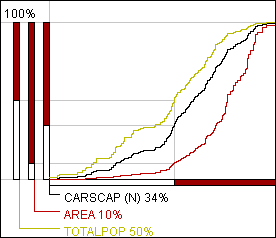
Abb. 12
Verallgemeinerte cumulative
Kurven werden für die Attribute "Area" (Bezirk) und "Total population
(absolut Bevölkerung) erstellt. Die Klassifikation wird auf der Basis des
Attributs "Number of cars per capita" (Anzahl der Autos pro Kopf)
durchgeführt.
Mit solch einem Werkzeug ist es einfach die Kriterien wie Gleichverteilung der Bevölkerung unter den Klassen, oder ungefähr gleich große, von den Klassen besetzte Bereiche, oder andere spezifische Kriterien, welche von diesem oder jenem angewendeten Bereich abhängen, darstellen. Um Klassen ungefähr gleich groß bezüglich der Bevölkerung zu machen, sollte sich ein Analytiker auf den Prozeß der Umbruchverschiebung auf der Achse bezüglich der Gesamtbevölkerung konzentrieren und versuchen die Position des Zeigers so zu setzten, daß die Achse in gleich lange Segmente eingeteilt ist.
Nebst dieser Möglichkeit, können verallgemeinerte cumulative Kurven dazu benutzt werden Verknüpfungen zwischen verschiedenen Charakteristika der Klassifizierten Objekte zu finden. Dies soll anhand eines Beispiels an der Arbeitslosigkeit von Leichestershire deutlich gemacht werden. Es werden die Attribute "Number of unemployment" (Anzahl der Arbeitslosen) und "Total populaiton" (absolute Bevölkerung) zur Berechnung des prozentualen Anteils der Arbeitslosen an der Bevölkerung in jedem Bezirk benutzt. Dann soll dieses neue Attribut die Basis der Klassifikation sein. Das Klassifikationswerkzeug zeigt an, daß die Proportionen von Arbeitslosen in der Bevölkerung zwischen 0.9% und 13.62% variiert. Betrachtet man nun die Werte über 4% als recht hoch, so könnte man nachschauen, in welchen Bezirken dieser Grenzwert überschritten wird. Dafür wird die Zahl 4 als Klassenumbruch eingetragen, wodurch alle Bezirke in 2 Klassen unterteilt werden: Mit bis zu 4% Arbeitslosen in der Bevölkerung und mehr als 4%. Die cumulative Kurve zeigt, daß nur 18% aller Bezirke zu der oberen Klasse gehören (Abb. 13). Die Karte zeigt eine klare räumliche Anhäufung solcher Bezirke im Zentrum der Region. Man erkennt, daß diese Bezirke einen eher kleinen Teil der ganzen Region einnehmen. Wenn jedoch das Attribut "Total population" (absolute Bevölkerung) zur Darstellung der cumulative Kurve ausgewählt wird, so sieht man, daß 33% der gesamten Bevölkerung von Leicestershire in diesen Bezirken mit hohem Arbeitslosenanteil lebt.
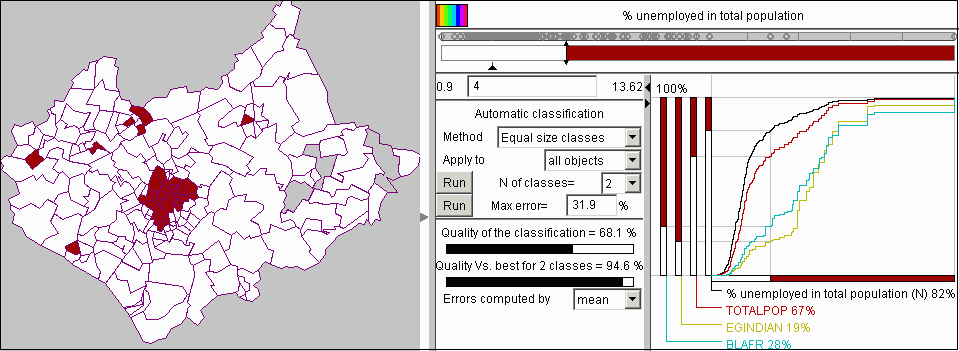
Abb. 13
Die Benutzung von
verallgemeinerten cumulative Kurven zur Erforschung der Arbeitslosenzahlen in
Leicestershire
Es ist auch interessant zu erfahren, ob es einen Link zwischen Arbeitslosigkeit und der Verteilung von nationalen Minderheiten vorhanden ist. Zur cumulative Kurvendarstellung wurde das Attribut BLAFR hinzugefügt, welches die absolute Anzahl der Personen von Afrika in den Bezirken darstellt. In Abb. 13 kann man deutlich sehen, daß sich die Kurve für diese Bevölkerungsgruppe deutlich von der für die gesamte Bevölkerung unterscheidet. Ebenso kann man sehen, daß die Achsen, welche dieses Attribut darstellen, in andere Proportionen als die für die Häufigkeit und für die gesamte Bevölkerung unterteilt ist. Nur 28% der Personen mit afrikanischer Abstammung leben in Bezirken mit weniger Arbeitslosen und, daher, leben 72% in Bezirken mit mehr als 4% Arbeitslose in der Bevölkerung. Der Unterschied ist sogar noch deutlicher für Menschen indischer Abstammung (dargestellt mit dem Attribut EGINDIAN). Man kann erkennen, daß 81% dieser Menschen in Regionen mit hoher Arbeitslosenquote leben.
Wenn man die Arbeitslosenzahlen weiter untersucht indem man den Klassenumbruch so verschiebt, daß die Bevölkerung in zwei gleich große Klassen unterteilt wird, bekommt man ein Ergebnis wie in Abb. 14. Der neue Wert des Klassenumbruchs liegt bei 2.89. Dies bedeutet, daß 50% der Bevölkerung in Bezirken mit mehr als 2.89% Arbeitslosen leben. Diese Bezirke, wie man auf der Karte erkennen kann, nehmen einen relativ kleinen Teil der Region ein. Demnach ist die Bevölkerungsdichte in ihnen höher als in den restlichen Bezirken. Scheinbar sind dies meistens Großstadtbezirke. Die Karte zeigt auch, daß die Bezirke mit hoher Arbeitslosenquote räumlich gebündelt sind. Die bereits erwähnten nationalen Minderheiten sind nun auf folgender Weise in den Klassen verteilt: nur 14% der Inder und 18% der Afrikaner leben in Bezirken mit niedriger Arbeitslosenquote und demnach wohnen 86% und 82% jeweils in den Bezirken mit mehr als 2.89% Arbeitslosen in der Bevölkerung.
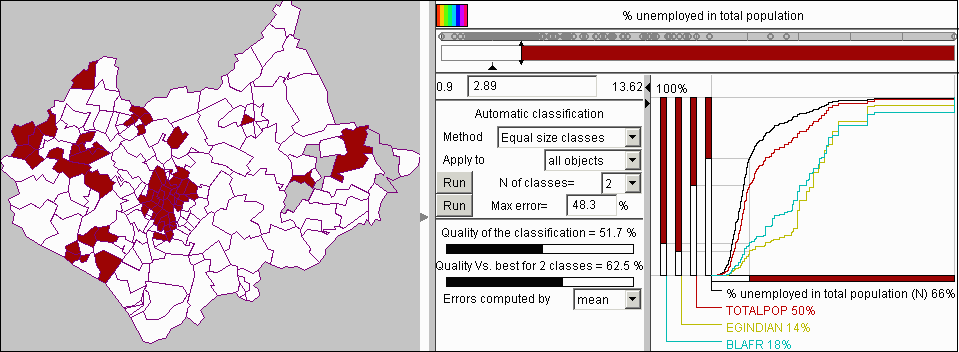
Abb. 14
Die cumulative Kurve stellt
die Trennung der Bezirke in zwei Klassen mit gleicher Bevölkerung dar.
Dieses analytische Beispiel demonstriert, daß verallgemeinerte cumulative Kurven die Klassifikation mit mehreren Kriterien erleichtert, sondern auch Verbindungen in diesen Daten aufdecken. Man sollte jedoch beachten, daß diese Technik nur für Attribute verwendet werden kann, deren Werte über die Menge der zugehörigen Objekte aufsummiert werden können. Zum Beispiel wäre es falsch diese Technik auf Prozentzahlen, Durchschnittswerte, Verhältnisse, Werte pro Kopf, etc. anzuwenden.
Innerhalb des Systems können mehrere graphische Darstellungen gleichzeitig auf dem Bildschirm abgebildet sein. Neben Karten können dies Punktegraphen, "Scatter"-Graphen und Graphen mit parallelen Koordinaten sein. Die Darstellungen können verschiedene Attribute des selben Objektes oder des selben Attributs in verschiedenen Arten oder Kombinationen darstellen. Mit einer Klassifikation ist es möglich die Klassenfarben auf andere Darstellungen zu übertragen. Als Ergebnis werden Punkte eines Punktegraphen, oder eines "Scatter"-Graphen, und Linien eines Graphen mit parallelen Koordinaten in den Farben der Klasse respektive der Objekte dargestellt. Diese Eigenschaft, bekannt als "brushing", ist sehr nützlich Verbindungen zwischen Attributen zu studieren. Dafür sollte "broadcast classification" aktiviert sein.
Das kleine Dreieck (Zeiger) zwischen dem zusammengesetzten Schieber und dem Textfeld zeigt die Referenzklasse an. Mitglieder dieser Klassen erscheinen in weiß. Die mit niedrigeren Werten werden z.B. in Blauschattierungen und die mit größeren Werte in Rotschattierungen dargestellt. Die Referenzklasse kann verändert werden, indem der Zeiger verschoben wird.
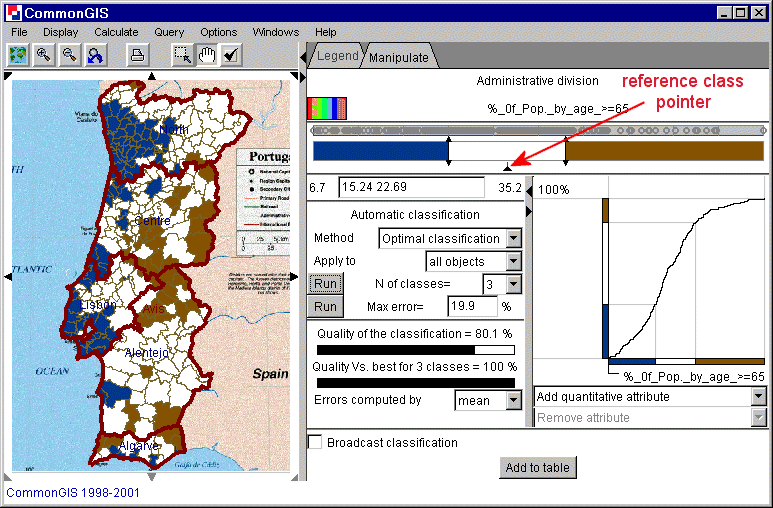
Abb. 15
Portugal - Klassifikation -
%_of_Pop_by_age_>=65
Ist einmal eine gewünschte Klassifikation erreicht, so kann sie als ein neues Attribut der Schicht (Tabelle) hinzugefügt werden. Jedem Objekt wird dann eine Zahl zugeordnet, welche der jeweiligen Klasse entspricht. Auf dieses neue Attribut könnten wiederum neue Methoden angewendet werden.
Mit diesem Werkzeug wird jeder Wert eines Attributes mit einem einzelnen Balken dargestellt, dessen Höhe proportional zum Wert ist. Die Farbe kann verändert werden, indem man auf das Kästchen neben dem Attributsnamen klickt. Standalone bars können so manipuliert werden, daß ein Vergleich zu einem Wert oder einem Objekt sichtbar wird. Um einen Wert mit den anderen zu vergleichen schiebt man den doppelseitigen Pfeil links neben dem Punktegraphen nach oben oder unten, oder man setzt den Wert in dem Textfeld "Compare to". Positive Werte werden oberhalb einer Linie gezeichnet, negative in der selben Farbe darunter (Abb. 16).
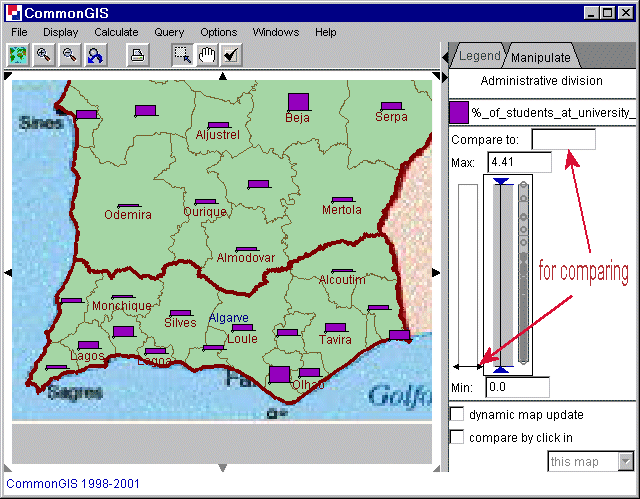
Abb. 16
Portugal, Süden - Standalone bars - %_of
_students_at_university_1991
Manchmal bestehen Attribute nicht aus numerischen Werten und eine Ordnung kann nicht erfolgen. Dann kann jeder Wert in einer Verschiedenen Farbe dargestellt werden. Diese Farben können auch verändert werden, indem auf das farbige Kästchen neben den Attributwerten geklickt wird. Ist das kleine Kästchen daneben nicht aktiviert, dann wird dieser Wert auch nicht auf der Karte dargestellt (dunkel graue Objekte). In Abb. 17 werden die verschiedenen Religionen in Europa dargestellt, wobei "Lutheran" nicht aktiv ist und somit in dunkel grau dargestellt wird (siehe Island, Norwegen, Dänemark, etc.).
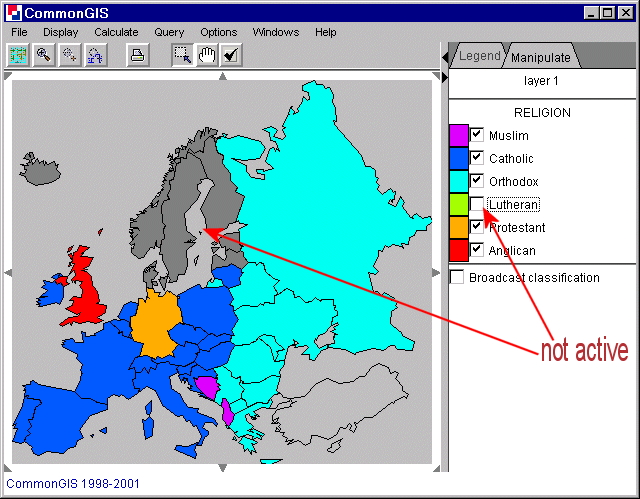
Abb. 17
Europa - Color - Religionen
Mit dieser Vergleichsmethode die ausgewählten Attribute werden in Balken nebeneinander dargestellt. Es ist nicht möglich einen oder mehrere davon zu betonen, wie in anderen Methoden (z.B. utility bars; erklärt hier). Die Farbveränderung oder das Vergleichen mit speziellen Werten wird hier wie in den anderen Methoden gehandhabt.
Wenn es sinnvoll ist Attribute zusammenzusetzen, da sie sich aufsummieren lassen, sind pie charts eine gute Visualisierungsmethode. Zum Beispiel ergibt das aufsummieren aller Altersgruppen die gesamte Population der jeweiligen Region.
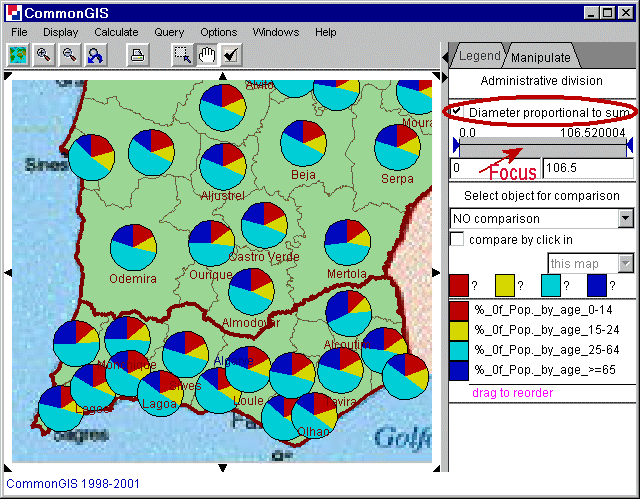
Abb. 18
Portugal - utility wheels -Altersgruppen
Die Reihenfolge der Attribute kann durch Ziehen mit der Maus verändert werden. Ein kleiner grüner Pfeil zeigt an, wo das Attribut plaziert wird, wenn es losgelassen wird. Die Farben können auch hier wieder durch klicken auf den farbigen Kästchen geändert werden. Um den Durchmesser des Kreises proportional zur Summe darzustellen aktiviere man das Kästchen "Diameter proportional to sum". Unter diesem Kästchen ist ein Balken, der fokussieren kann. Dabei werden große Kreise entfernt und kleinere werden vergrößert und somit besser sichtbar. Diese Aktion macht besonders Sinn, wenn die Durchmesser proportional zur Summe sind.
Zwei ausgewählte Attribute können durch Dreiecke visualisiert
werden. Welche Achse zu welchem Attribut gehört, wird in dem mittleren
Teil der Legende durch kleine doppelseitige Pfeile dargestellt. Das Beispiel in
Abb. 19 kann man wie folgt erkennen: vertikal (hoch/runter): Beginner level
runs in % (Anfängerpisten in %); horizontal (rechts/links): Price for ski
pass (6 days) (Preis für Skipaß für 6 Tage). Die Zahlen neben
den Dreiecken in der Legende sind die Extremwerte jedes Attributes. Rechts
werden die Werte für das vertikal aufgetragene Attribut angezeigt,
darunter die für das horizontal aufgetragene Attribut. Die vier Dreiecke
zeigen die extremen Formen, welche ein Dreieck annehmen könnte:
oben
links: Maximum an Anfängerpisten und Minimum des Preises;
unten links:
Minimum beider Attribute;
oben rechts: Maximum beider Attribute;
unten
rechts: Minimum der Anfängerpisten und Maximum des Preises.
Jemand, der zum ersten mal Skifahren geht und dabei möglichst wenig
Zahlen möchte, sollte auf hohe, schmale Dreiecke achten. Vermutlich
wäre das dann La Forclaz (schwarzer Kreis beim Mauszeiger).
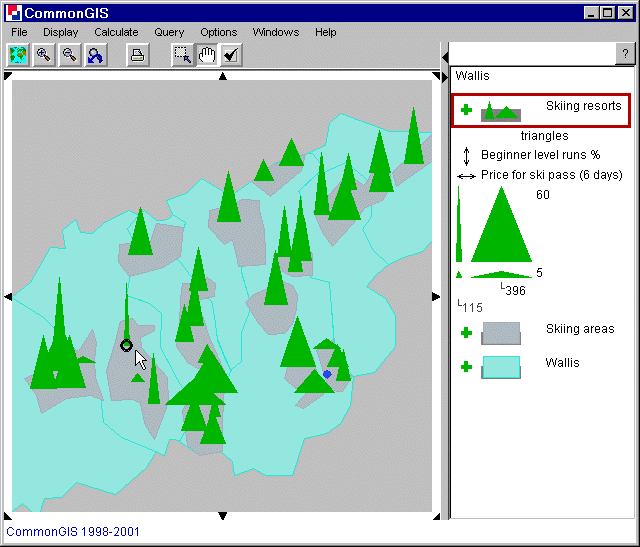
Abb. 19
Wallis - Triangles
Die Eigenschaften der Dreiecke kann durch ein Doppelklick auf die Dreiecke in der Legende geändert werden. Diese wären, Farbe, minimale und maximale Höhe und Weite.
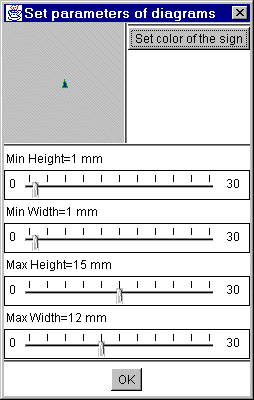
Abb. 20
Dreieckseigenschften
Die Visualisierung von utility bars ist den standalone bars sehr ähnlich, nur können mehrere Attribute mit Hilfe des Textfeldes unten rechts hinzugefügt werden. Verschiedene Attribute werden in verschiedenen Farben dargestellt, welche durch Doppelklick auf das farbige Kästchen geändert werden können. Das Vergleichen eines Objektes mit anderen kann durch Auswählen von der "Select object for comparison" Liste geschehen oder mit "compare by click in".
Jedem Attribut können verschiedene Gewichte zugeordnet werden. Dazu muß der Schieber unter dem Attributnamen verschoben werden. Das momentane Gewicht wird rechts davon angezeigt. Der Knopf "Set equal weights" gibt allen Attributen die gleichen Gewichte. Der Pfeil links von dem Attributnamen gibt an, ob das Attribut maximiert oder minimiert werden soll. Zeigt der Pfeil nach oben rechts, so soll maximiert werden (Profit: größere Werte sind besser). Zeigt er nach unten rechts, so soll minimiert werden: (Kosten, kleinere Werte sind besser).
Je nach Gewicht und Optimierungsrichtung (Min oder Max), berechnet Descartes die Ergebnisse durch Integration über die Fläche des Rahmens der Balken und sortiert diese mit prozentualen Werten. In dem grauen Balken über den Gewichtregelungen, kann man entscheiden, welche utility bars auf der Karte angezeigt werden. Dazu mehr unter Entscheidungshilfe.
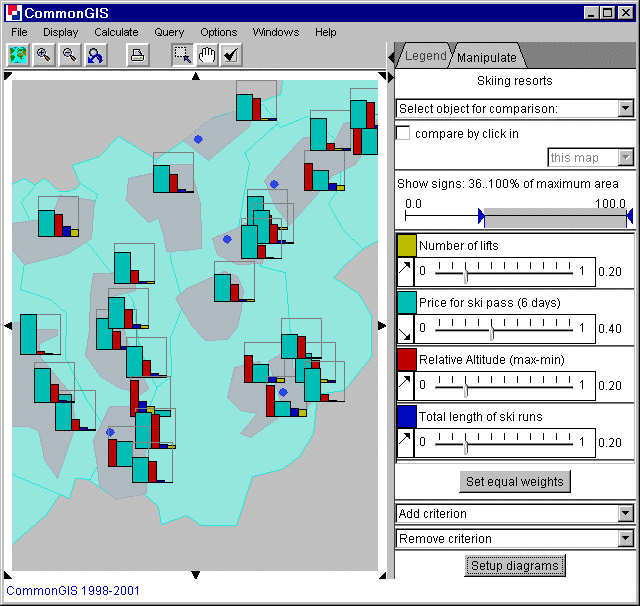
Abb. 21
Wallis - utility bars
Um die Parameter der Diagramme zu ändern klickt man auf "Setup diagrams" (siehe Abb. 22). Hier kann die maximale Höhe und Weite angegeben werden. Ein Rahmen, eine dünne Linie um die Maximalwerte kann mit "Frame the sign" aktiviert werden. Die Reihenfolge der einzelnen Balken kann vorgeschrieben werden: "preserved": behält die Reihenfolge bei, "descending": sortiert nach Verminderung der Höhe, "ascending": sortiert nach Anstieg der Höhe.
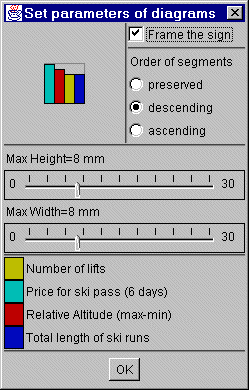
Abb. 22
Utility bar Eigenschaften
Utility wheels sind genau wie utility bars. Die Manipulationsmethoden sind die gleichen, außer, daß anstatt Balken Kreise auf der Karte dargestellt werden. Der Radius eines Kreises Entspricht der Höhe eines Balkens und der Winkel der Breite.